فرمول محاسبه حجم و مساحت (کره، مخروط و استوانه)
ناشر: مینویسم (minevisam.ir)
نویسنده: مهدیه حسینی ها
تاریخ انتشار: 30 می 2021
تماس با ما: ارسال پیام
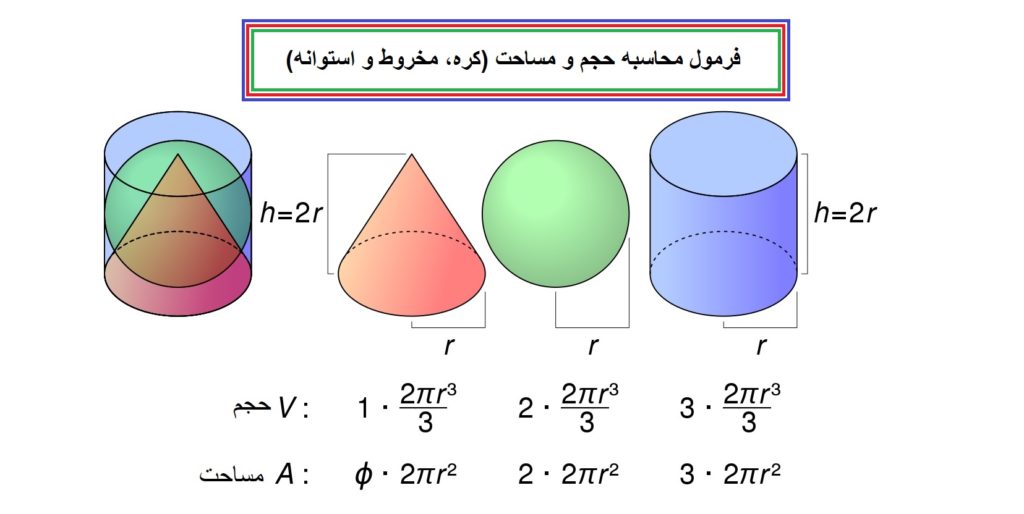
در این مطلب می توانید فرمول محاسبه حجم و مساحت اشکال هندسی سه بعدی مانند کره، مخروط و استوانه مشاهده نمایید و همچنین تعاریف این اشکال هندسی را مطالعه نمایید.
فرمول حجم و مساحت کره
کُره یا سِپِهر یک جسم هندسی کاملاً گرد در فضای سه بعدی است. برای نمونه توپ یک کره است. برای بدست آوردن مساحت جانبی و مساحت کل هر شکل از اشکال هندسی سه بعدی و دارای حجم ، می توان از رسم گسترده آن یعنی باز کردن آن در فضای دو بعدی و بر روی صفحه و محاسبه مساحت هر یک از سطوح استفاده کرد.
برای به دست آوردن مساحت و حجم کره ای با شعاع r باید از فرمول های زیر استفاده نمایید:
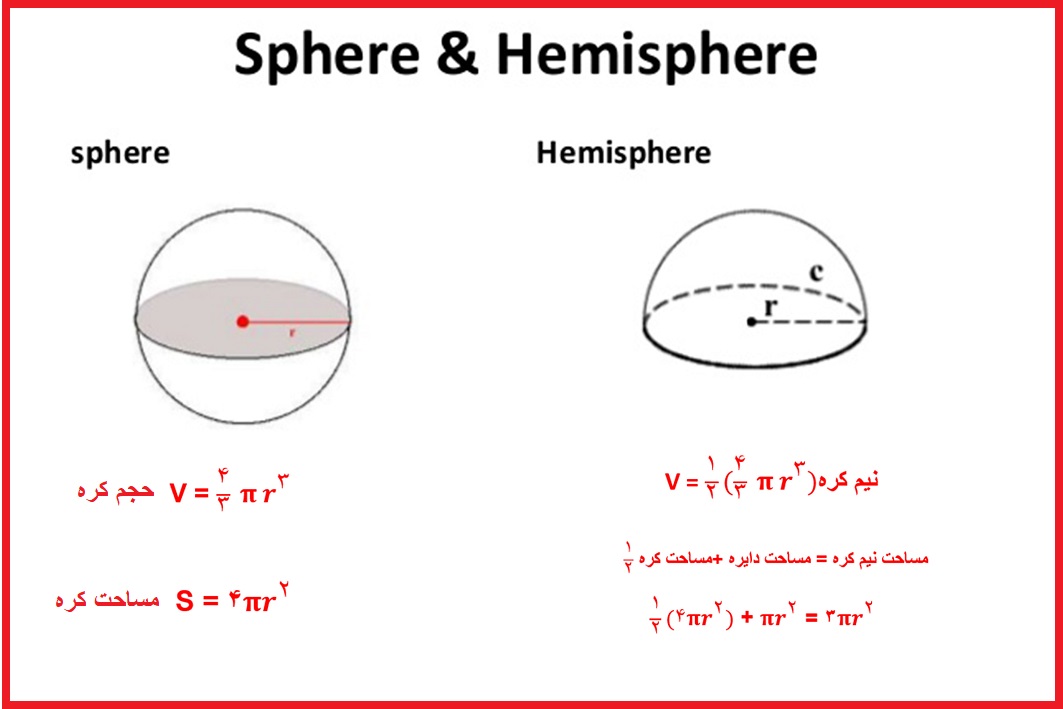
فرمول حجم و مساحت کره و نیمکره
کره چیست؟
شکل هندسی دایره مجموعه نقاطی از صفحه است که همه آن نقاط از یک نقطه در همان صفحه به نام مرکز به یک فاصله است. و به این اندازه ثابت، شعاع می گویند.
کُره یا گوی یا سِپِهر یک جسم هندسی کاملاً گرد در فضای سه بعدی است. برای نمونه توپ یک کره است. کره مانند دایره که در دو بعد است، در فضای سه بعدی یک کاملاً متقارن در گرداگرد یک نقطه است. تمام نقاطی که بر سطح کره قرار دارند در فاصلهٔ یکسان از مرکز کره قرار دارند.
از دوران یک نیم دایره حول قطر آن، یک کره بوجود می آید. کره، مجموعه نقاطی از فضاست که همه آن نقطه ها از یک نقطه به نام مرکز به یک فاصله ثابت و مشخص هستند. به این اندازه ثابت، شعاع کره می گویند.
ویژگی های کره
- همه نقاط روی کره به فاصلهای یکسان از مرکز کره قرار میگیرند.
- فاصله ثابت نقاط روی کره تا مرکز آن شعاع کره نامیده میشود.
- فاصله بین یک نقطه روی کره تا نقطه مقابل آن (با عبور از مرکز) قطر کره نامیده میشود.
- قطر کره دو برابر اندازه شعاع آن است.
فرمول حجم و مساحت جانبی استوانه
برای به دست آوردن حجم و مساجت جانبی استوانه از فرمول های زیر استفاده کنید:
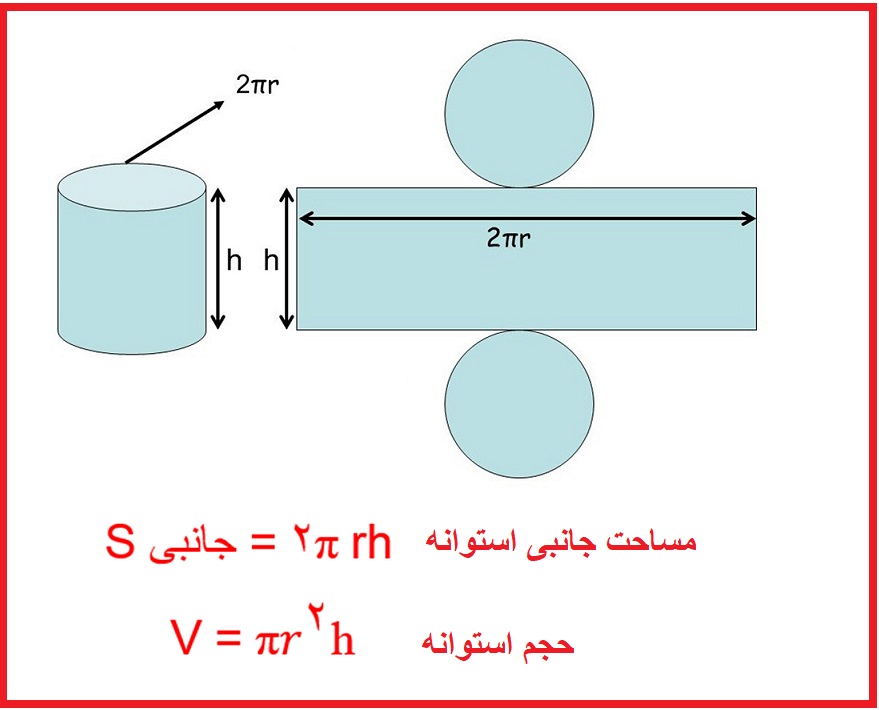
فرمول و نحوه محاسبه حجم و مساحت جانبی استوانه
استوانه چیست؟
استوانه یا سُتوُن یکی از پایهایترین شکلهای منحنی فضایی در هندسه می باشد که سطح دور آن را مجموعه نقاطی تشکیل میدهد که در فاصلهٔ یکسان از یک خط راست قرار دارند، این خط راست محور نام دارد. دو سر این شکل فضایی به کمک دو صفحهٔ عمود بر محور استوانه بسته میشود. یعنی از دوران مستطیل حول اضلاع آن، استوانه بدست می آید. در این صورت قاعده آن به شکل دایره خواهد شد. و شعاع دایره همان شعاع استوانه خواهد بود.
ویژگی های استوانه
- یکی از وجههای استوانه منحنی است.
- دو سر استوانه توسط قاعدههای دایرهای شکل آن احاطه شدهاند.
- هر دو قاعده استوانه دقیقاً یک شکل و یک اندازه هستند.
- خط راست عمود بر هر دو قاعده استوانه ارتفاع آن نامیده میشود.
- با توجه به منحنی بودن یکی از وجوه استوانه، این شکل چند وجهی محسوب نمیشود
فرمول حجم و مساحت مخروط
مخروط چیست؟
مخروط Cone یکی از گونههای هرم است که قاعدهٔ آن دایره می باشد. مخروط ها میتوانند به صورت قائم یا اریب باشند. یک مخروط یک شکل هندسی سهبُعدی می باشد که از پایهٔ تختش (سطح مقطع مخروط) به آرامی یا به سرعت (به سطح قاعده و ارتفاع بستگی دارد) تا راس باریک میشود. مخروط شکلی جامد است که به یک صفحهٔ پایه (سطح مقطع مخروط)، محدود میشود و سطح جانبی آن نیز مکان هندسی خطوط راستی است که نوک مخروط را به نقاط پیرامون پایه (سطح مقطع) پیوند میزنند.
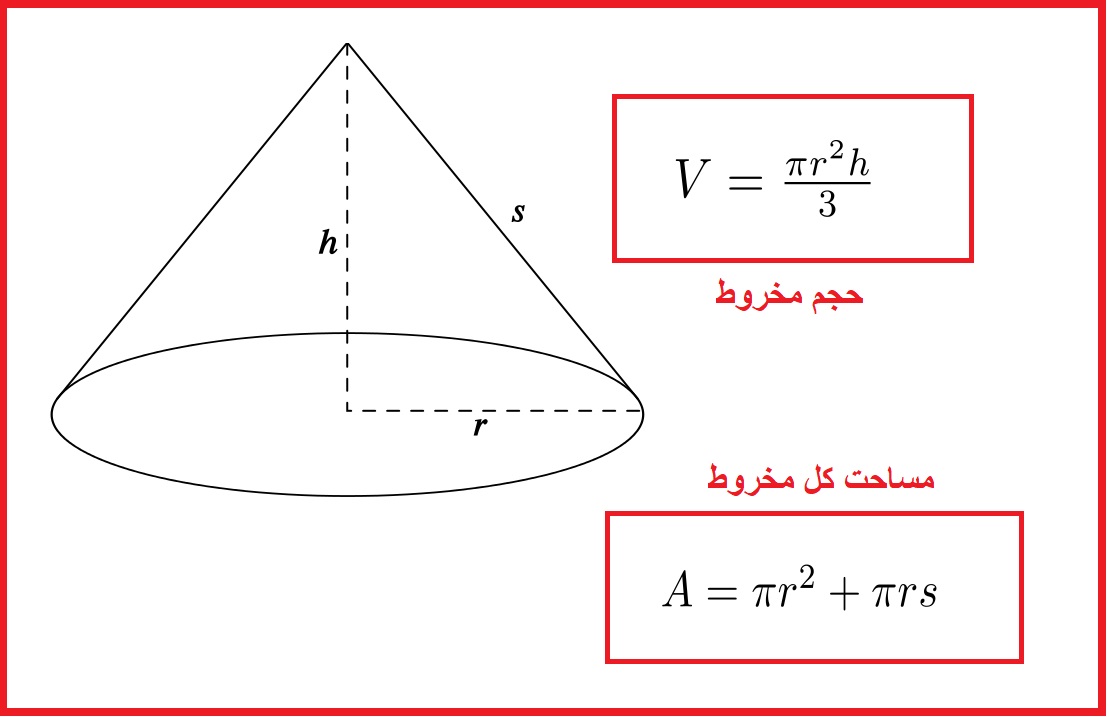
فرمول حجم و مساحت مخروط






