فرمول محاسبه مساحت و محیط شش ضلعی منتظم سوم ابتدایی + مثال عددی
ناشر: مینویسم (minevisam.ir)
نویسنده: مهدیه حسینی ها
تاریخ انتشار: 22 اکتبر 2020
تماس با ما: ارسال پیام

در این مطلب فرمول محاسبه مساحت و محیط شش ضلعی منتظم برای سوم ابتدایی را در اختیار شما عزیزان قرار می دهیم. شکل هندسی شش ضلعی (Hexagon) شکلی است که دارای شش زاویه (گوشه) و شش ضلع می باشد. مجموع زوایای داخلی در یک شش ضلعی برابر ۷۲۰ درجه می باشد. شش ضلعی دارای انواع مختلفی می باشد که شامل ششضلعی منتظم و غیرمنتظم و ششضلعی محدب و مقعر می باشد.
بیشتر بخوانید : چگونه به کودکانمان جدول ضرب را یاد دهیم؟
شما می توانید برای یادآوری فرمول های ساده ریاضی که برای محاسبه محیط و مساحت اشکال هندسی ساده همچون مربع و مستطیل و دایره و … به سایت می نویسم مراجعه کنید و مجدد آن را بخوانید و به خاطر بسپارید.
فرمول مساحت شش ضلعی سوم دبستان
ویژگی شش ضلعی منتظم این است که زاویههای داخلی آن ۱۲۰ درجه است و زاویههای خارجی آن ۶۰ درجه می باشد. برای محاسبه مساحت شش ضلعی منتظم می توانید از فرمول زیر استفاده نمایید:
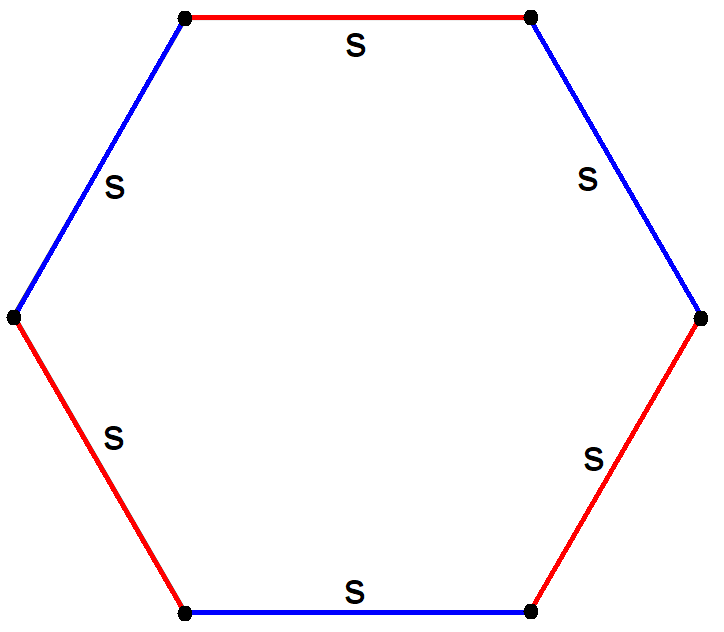
اندازه هر ضلع شش ضلعی برابر است با s
مساحت شش ضلعی منتظم (مساحت شکل فوق) را از فرمول زیر محاسبه کنید.
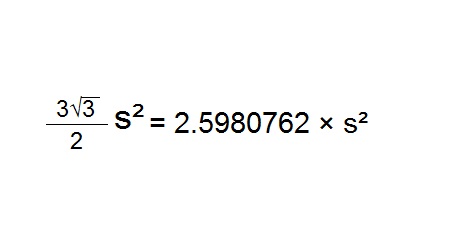
فرمول مساحت فرمول شش ضلعی
مساحت شش ضلعی منتظم = ²(اندازه یک ضلع)× 2 ÷ 3 × 3√
فرمول محیط شش ضلعی منتظم برای سوم ابتدایی
برای محاسبه محیط شش ضلعی منتظم نیز کافی است اندازه هر 6 ضلع را با هم جمع کنید و از آنجا که اندازه هر 6 ضلع در شش ضلعی منتظم با هم برابر است از فرمول : یک ضلع ×۶ استفاده کنید.
محیط شش ضلعی منتظم = 6 × اندازه یک ضلع
مثال برای محاسبه محیط و مساحت شش ضلعی منتظم
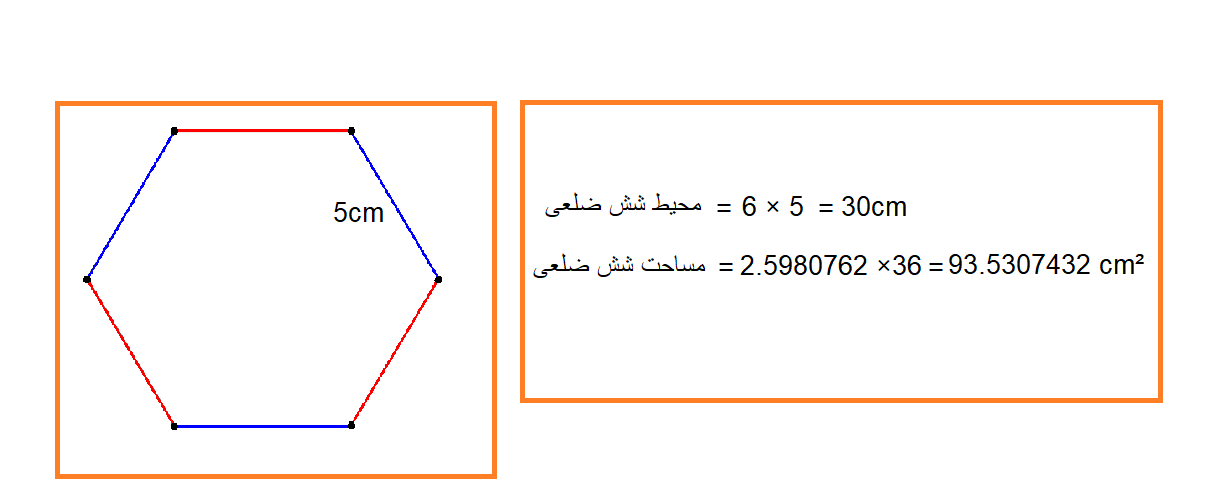
مثال برای محاسبه محیط و مساحت شش ضلعی منتظم
آشنایی با انواع شش ضلعی
مشخصات شکل شش ضلعی این است که هیچ یک از اضلاع آن خمیده نباشند. (به همین دلیل دایره نمیتواند یک ششضلعی یا بهطورکلی چندضلعی باشد!) و همچنین باید همه خطوط و اضلاع آن به هم متصل باشند. در ادامه با انواع شش ضلعی ها آشنا خواهید شد.
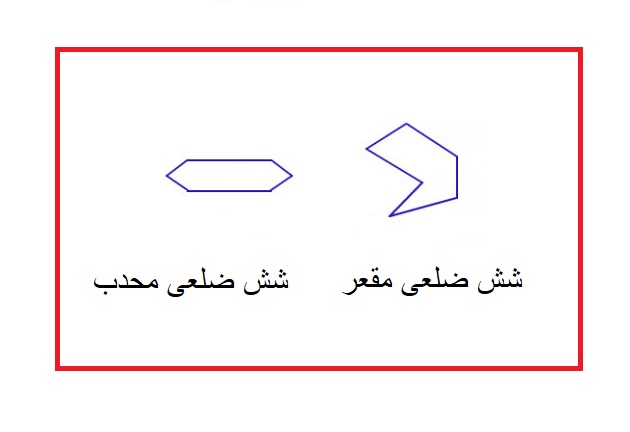
شش ضلعی محدب و مقعر
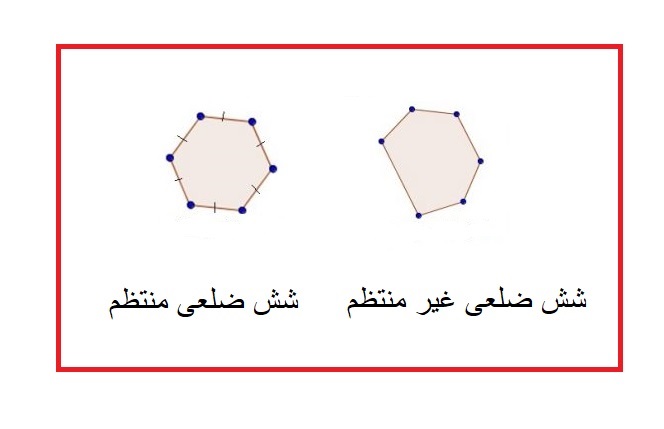
شش ضلعی منتظم و غبر منتظم
فرمول محاسبه محیط انواع شش ضلعی ها برابر است تا مجموع طول اضلاع، اما فرمول محاسبه مساحت شش ضلعی غیر منتظم ، شش ضلعی محدب و مقعر متفاوت است و باید آن را به یک چند شکل هندسی تبدیل کرد و با توجه به شکل از فرمول مخصوص به خود مساحت آن را حاسبه نمود و در آخر باهم جمع کرد.






